Scroll、Polygon zkEVM 使用或將使用基於 EVM 的 zk 電路,zk Proof 將在其證明器上進行的每一筆交易或者一大包交易中生成,雖然這能讓開發者建立「全鏈上」的應用程式,但它能否高效且經濟地執行高效能的應用程式呢?
(前情提要:zkEVM有哪五大常見類型?項目進展一次看)
(背景補充:V神發表「zk-EVM多客戶端」:可保護以太坊L1,透過AI加速證明、容錯)
關於以太坊虛擬機器(EVM)的效能
在以太坊主網上的每一個操作都要花費一定的 Gas,如果我們把跑基礎應用所需的計算量都放在鏈上,要麼 App 會崩潰,要麼使用者會破產。
這催生了 L2 :OPRU 引入了排序器來捆綁一堆交易,然後提交到主網上。這不僅有助於 app 承接以太坊的安全性,同時也給予了使用者更好的體驗。使用者可以更快地提交交易,手續費也更加便宜了。雖然操作變得便宜了,但它仍然使用原生 EVM 作為執行層。
和 ZK Rollups 類似,Scroll、Polygon zkEVM 使用或將使用基於 EVM 的 zk 電路,zk Proof 將在其證明器上進行的每一筆交易或者一大包交易中生成。雖然這能讓開發者建立「全鏈上」的應用程式,但它是否仍能高效且經濟地執行高效能的應用程式呢?
這些高效能應用都有哪些?
人們首先想到的是遊戲、鏈上訂單簿、Web3 社交、機器學習、基因組建模等。所有這些都需要大計算量,在 L2 上執行也會非常昂貴。EVM 的另一個問題是,計算的速度和效率不如現在的其他系統,如 SVM (Sealevel Virtual Machine)。
雖然 L3 EVM 可以使計算更便宜,但 EVM 本身的結構可能不是執行高計算的最佳方式,因為它無法計算並行運算。在上面每建一個新的層的時候,為了保持去中心化的精神,就需要建立新的基礎設施(新的節點網路),這仍然需要同樣數量的提供者來擴充套件,或者是一組全新的節點提供者(個人 / 企業)來提供資源,或者兩者都需要。
因此,每當更先進的解決方案被建立時,現有的基礎設施就要被升級,或者在上面建立一個新的層。為了解決這個問題,我們需要一個後量子安全、去中心化、無需信任、高效能的計算基礎設施,可以真正高效地使用量子演算法為去中心化的應用進行計算。
像 Solana、Sui 和 Aptos 這樣的 alt-L1s 能夠實現並行執行,但由於市場情緒,流動性短缺市場上缺乏開發人員,他們不會對以太坊產生挑戰。因為缺乏信任,而且以太坊用網路效應建立的護城河是里程碑式的。到目前為止,ETH/EVM 的殺手並不存在。這裡的問題是,為什麼所有的計算都應該在鏈上?是否存在一個同樣無需信任、去中心化的執行系統?這是 DCompute 系統能夠實現的。
DCompute 基礎設施要做到去中心化、後量子安全,也要做到無信任,不需要或者說不應該是區塊鏈 / 分散式技術,但驗證計算結果,正確的狀態轉換和最終確認是非常重要的。EVM 鏈的執行就是如此,在保持網路的安全性和不可篡改性的同時,去中心化的、無需信任的、安全的計算可以被移到鏈下。
我們在這裡主要忽略的是資料可用性的問題。這篇文章並非不關注資料的可用性,因為像 Celestia 和 EigenDA 這樣的解決方案已經在朝這個方向發展。
1. 只將計算外包(Only Compute Outsourced)
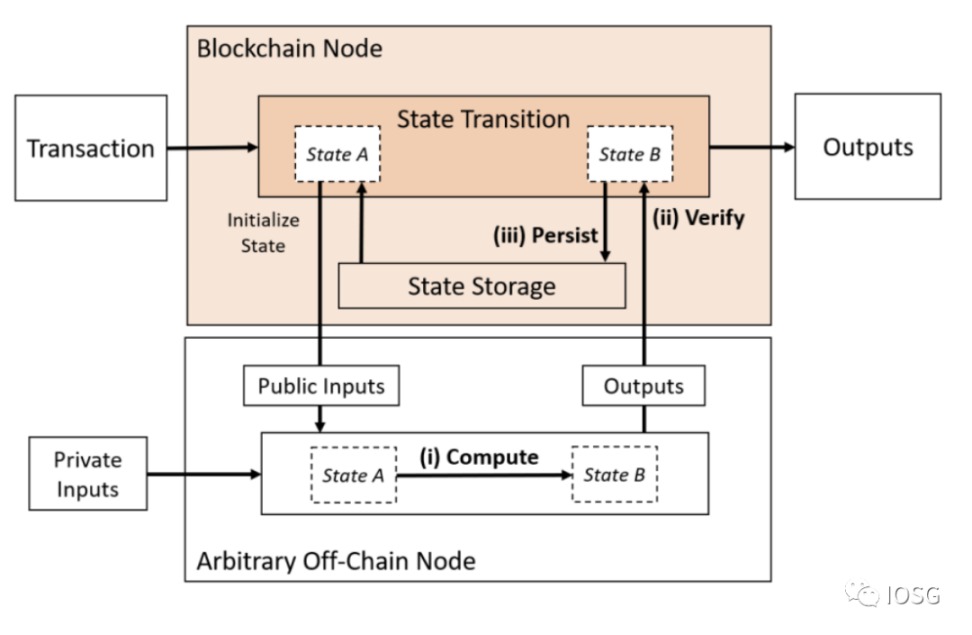
2. 將計算與資料可用性外包
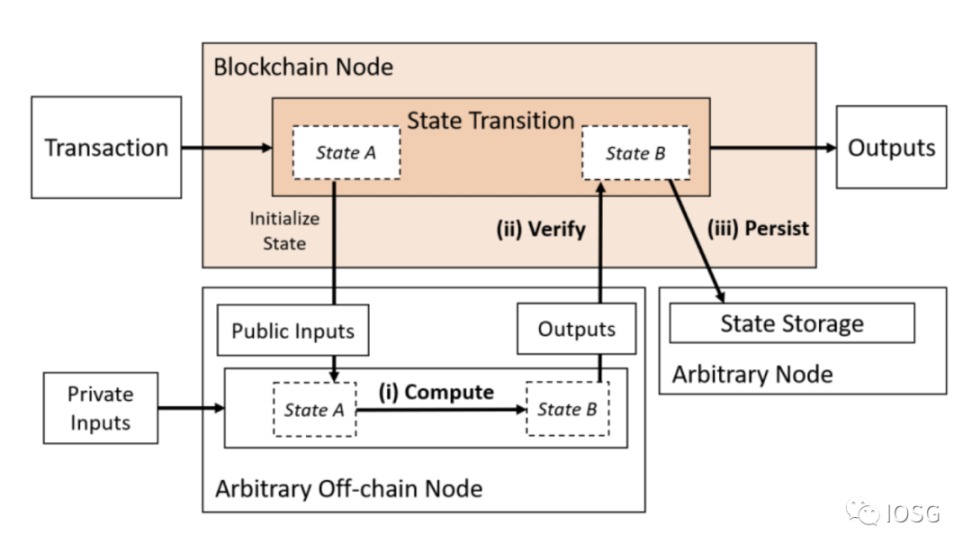
當我們看到 Type 1 時,zk-rollups 已經在做這個,但它們要麼受限於 EVM,要麼需要教導開發者學習全新的語言 / 指令集。理想的解決方案應該是高效的、有效的(成本和資源)、去中心化的、私密的和可驗證的。ZK 證明可以在 AWS 伺服器上構建,但它們並不是去中心化的。像 Nillion 和 Nexus 這樣的解決方案正在嘗試以去中心化的方式解決通用計算的問題。但這些解決方案是無法驗證的,如果沒有 ZK 證明的話。
Type 2 將鏈下計算模型與保持分離的資料可用性層結合起來,但計算仍然需要在鏈上進行驗證。
讓我們來看一下今天可用的不完全可信和可能完全無信任的不同去中心化計算模型。
其他計算系統(Alternative Computation Systems)
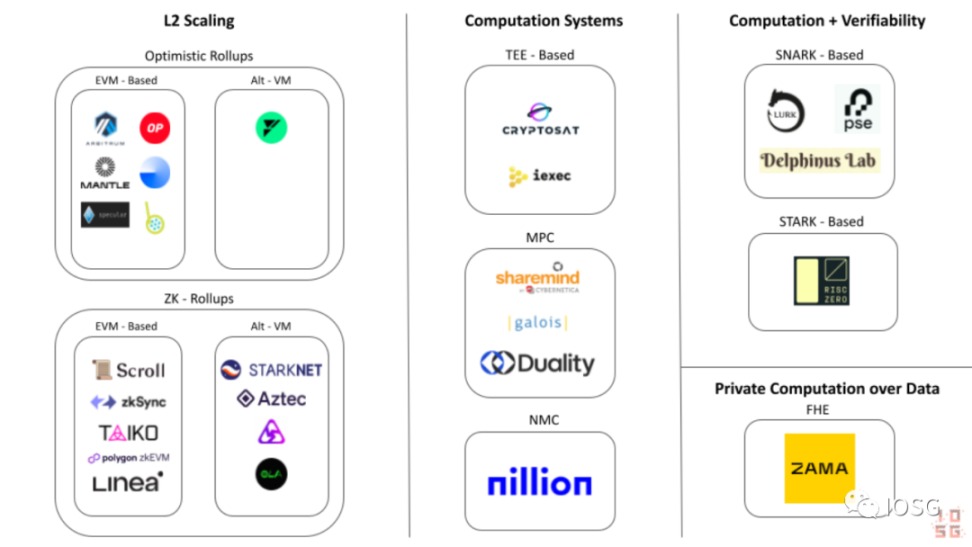
安全飛地計算(Secure Enclave Computations)/ 可信執行環境(Trusted Execution Environments)
TEE(可信執行環境)就像電腦或智慧手機內部的一個特殊盒子。它有自己的鎖和鑰匙,只有特定的程式(稱為可信應用程式)才能訪問。當這些可信應用程式在 TEE 內部執行時,它們就受到其他程式甚至作業系統本身的保護。
這就像一個只有幾個特殊朋友可以進入的祕密藏身處。TEE 最常見的例子是安全隔離區,它們存在於我們使用的裝置上,例如蘋果的 T1 晶片和英特爾的 SGX,用於在裝置內部執行關鍵操作,如 FaceID。
由於 TEE 是隔離的系統,認證過程無法被破壞,因為認證中存在信任假設。可以將其想象為存在一個安全門,你相信它是安全的,因為 Intel 或 Apple 建造了它,但世界上有足夠多的安全破壞者(包括駭客和其他電腦),可以破壞這扇安全門。TEE 不是「後量子安全」的,這意味著擁有無限資源的量子電腦可以破解 TEE 的安全性。隨著電腦迅速變得更加強大,我們必須在構建長期計算系統和密碼學方案時牢記後量子安全性。
安全多方計算 (SMPC)
SMPC(安全多方計算)也是區塊鏈技術從業熟知的一種計算方案,在 SMPC 網路中大致的工作流程會有如下 3 部分組成:
步驟 1 :將計算的輸入轉換為份額(shares),並分佈在 SMPC 節點之間。
步驟 2 :進行實際的計算,通常涉及 SMPC 節點之間的訊息交換。在此步驟結束時,每個節點將擁有計算輸出值的一個份額。
步驟 3 :將結果份額傳送到一個或多個結果節點,這些節點執行 LSS(祕密分享恢復演算法)以重構輸出結果。
想象一個汽車生產線,汽車的構建和製造元件(發動機、車門、後視鏡)被外包給原始裝置製造商(OEM)(工作節點),然後有一個裝配線,將所有元件組裝在一起製造汽車(結果節點)。
祕密分享 (Secret sharing) 對於保護隱私的去中心化計算模型非常重要。這可以防止單個參與方獲得完整的「祕密」(在這種情況下是輸入),並惡意產生錯誤的輸出。SMPC 可能是最容易和最安全的去中心化系統之一。雖然目前不存在一個完全去中心化的模型,但從邏輯上講這是有可能的。
像 Sharemind 這樣的 MPC 提供商為計算提供 MPC 基礎設施,但提供商仍然是集中的。如何確保隱私,如何確保網路 (或 Sharemind) 沒有惡意行為?這就是 zk 證明和 zk 可驗證計算的由來。
Nil Message Compute(NMC)
NMC 是由 Nillion 團隊開發的一種新的分散式計算方法。它是 MPC 的升級版,其中節點無需通過通過結果互動來進行通訊。為此,他們使用了一種稱為一次掩碼(One-Time Masking)的密碼原語,利用一系列稱為遮蔽因子(blinding factors)的隨機數來掩蓋一個 Secret,類似於一次性填充。OTM 旨在以高效的方式提供正確性,這意味著 NMC 節點不需要交換任何訊息來執行計算。這意味著 NMC 不會有 SMPC 的可擴充套件性問題。
零知識可驗證計算
ZK 可驗證計算(ZK Verifiable Computation)是對一組輸入和一個函式生成零知識證明,並證明任何系統執行的計算都會是正確執行的。儘管 ZK 驗證計算是新生事物,但它已經是以太坊網路擴充套件路線圖中一個非常關鍵的部分。
ZK 證明有各種各樣的實現形式(如下圖所示,根據論文「Off-Chaining_Models」中總結):
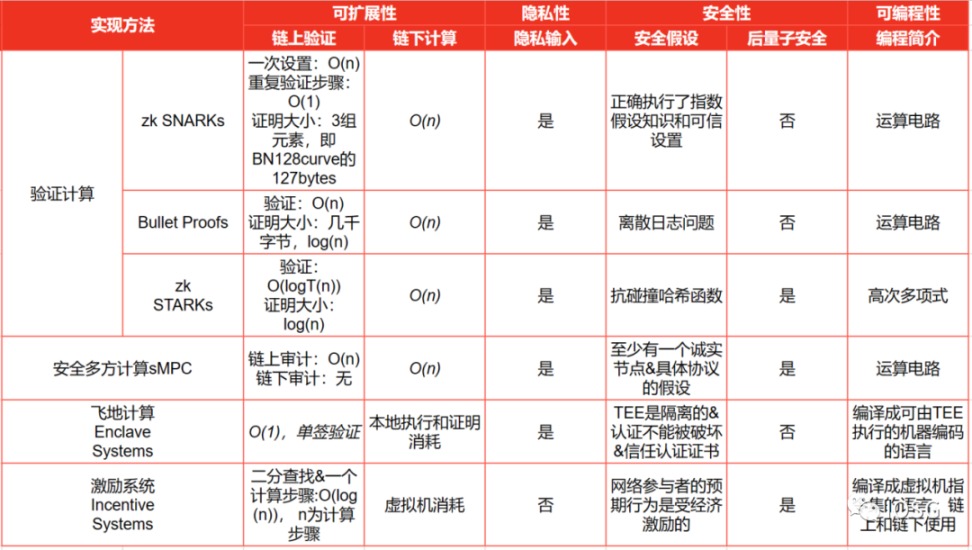
上面我們對 zk 證明的實現方式有了基本的瞭解,那麼使用 ZK 證明驗證計算需要什麼條件呢?
首先,我們需要選擇一個證明原語,理想的證明原語生成證明的成本低,對記憶體的要求不高,並且要易於驗證
其次,選擇一種 zk 電路,設計用於通過計算生成上述原語的證明
最後,在某個計算系統 / 網路中通過提供的輸入對給定的函式進行計算並給出輸出。
開發者的難題 – 證明效率困境
另外一個不得不說的事情就是構建電路的門檻還是很高,讓開發者學習 Solidity 已經不是一件容易的事情,現在要求開發者學習 Circom 等來構建電路,或者學習一門特定的程式語言 (如 Cairo) 來構建 zk-apps,這似乎是一個遙不可及的事情。
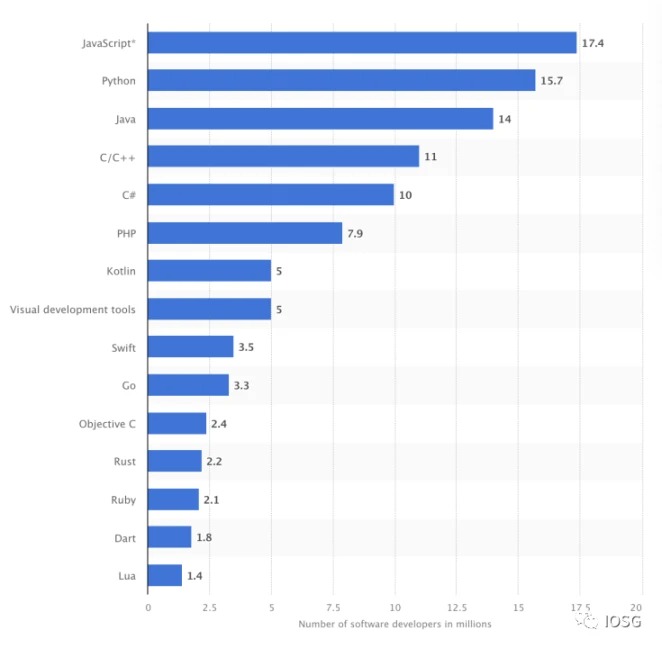
如上面的統計資料顯示,將 Web3 的環境改造得更適於開發,似乎比將開發人員引入新的 Web3 開發環境更具可持續性。
如果 ZK 是 Web3 的未來,Web3 應用程式需要使用現有的開發人員技能來構建,那麼 ZK 電路就需要這樣設計:支援由 JavaScript 或 Rust 等語言編寫的演算法執行的計算生成證明。
這樣的解決方案確實存在,筆者想到的是兩個團隊:RiscZero 和 Lurk Labs。兩個團隊都有一個非常相似的願景,即他們允許開發人員無需經歷陡峭的學習曲線即可構建 zk-app。
Lurk Labs 還處於早期階段,但該團隊已經在這個專案上工作了很長時間。他們專注於通過通用電路生成 Nova 證明(Nova Proof)。
Nova 證明是由卡耐基梅隆大學的 Abhiram Kothapalli 和微軟研究院的 Srinath Setty 以及紐約大學的 Ioanna Tziallae 提出的。與其他 SNARK 系統相比,Nova 證明在進行增量可驗證計算 (IVC) 方面具有特殊優勢。增量可驗證計算 (IVC) 是電腦科學和密碼學中的一個概念,旨在實現計算的驗證,而無需從頭開始重新計算整個計算。當計算時間長且複雜時,需要針對 IVC 對證明進行優化。
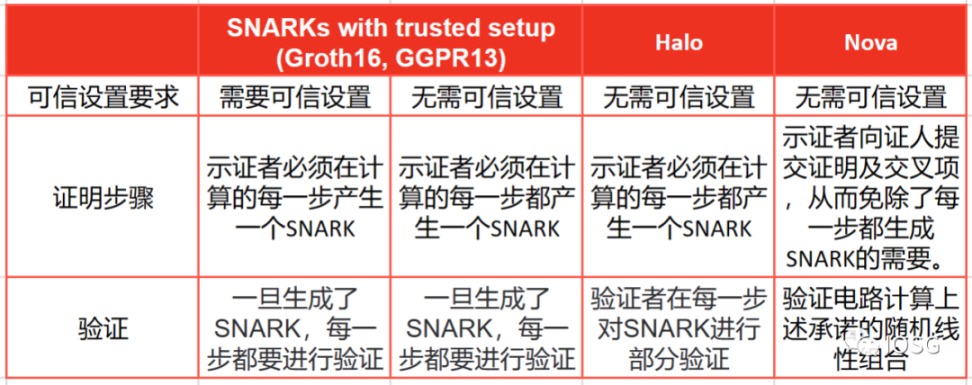
Nova 證明不像其他證明系統那樣「開箱即用」, Nova 只是一個摺疊技巧,開發者仍需要一個證明系統來生成證明。這就是為什麼 Lurk Labs 構建了 Lurk Lang,這是一個 LISP 實現。由於 LISP 是一種較低階的語言,它使得在通用電路上生成證明很容易,並且也很容易轉譯成 JavaScript,這將幫助 Lurk Labs 獲得 1740 萬 Javascript 開發者的支援。也支援其他通用語言,如 Python 的轉譯。
總而言之,Nova 證明似乎是一個偉大的原始證明系統。雖然它們的缺點是證明的大小隨著計算的大小線性增加,但另一方面,Nova 證明有進一步的壓縮空間。
STARK 證明的大小不會隨著計算量的增加而增加,因此它更適合驗證非常大的計算。為了進一步改善開發人員的體驗,他們還發布了 Bonsai 網路,這是一個分散式計算網路,由 RiscZero 生成的證明進行驗證。這是一個簡單的示意圖,代表 RiscZero 的 Bonsai 網路的工作原理。
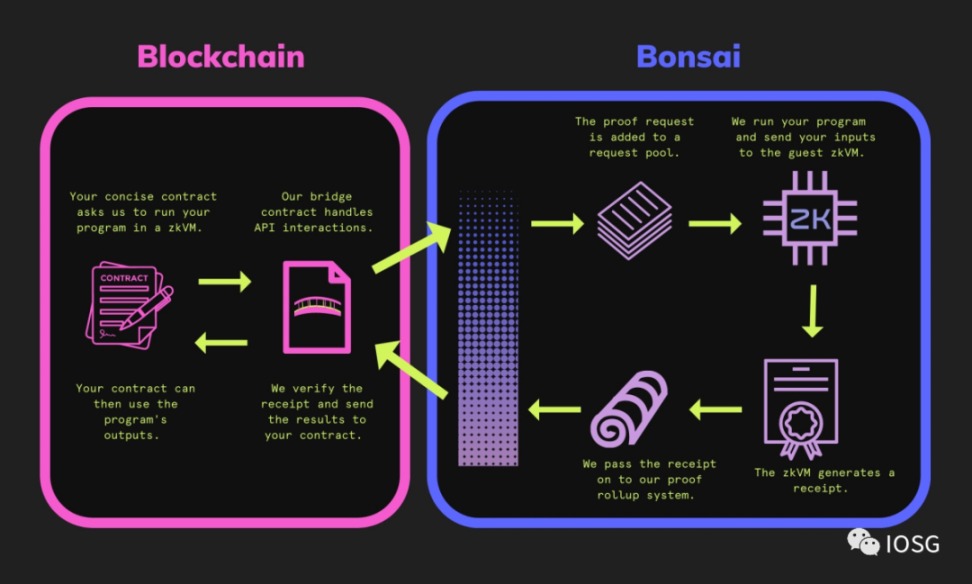
Bonsai 網路設計的美妙之處在於計算可以初始化,驗證,輸出全部做到鏈上。所有這些聽起來都像是烏托邦,但 STARK 證明也帶來了問題 —— 驗證成本太高。
Nova 證明似乎非常適合重複計算 (它的摺疊方案經濟高效) 和小型計算,這可能使 Lurk 成為 ML 推理驗證的一個很好的解決方案。
誰是贏家?


一些 zk-SNARK 系統在初始設定階段需要一個可信的設定過程,生成一組初始引數。這裡的信任假設是,可信的設定是誠實執行的,沒有任何惡意行為或篡改。如果受到攻擊,可能會導致建立無效的證明。
STARK 證明假設低階測試的安全性,用於驗證多項式的低階性質。它們還假設 hash 函式表現得像隨機預言機一樣。
兩個系統的正確實施也是一個安全假設。
- SMPC 網路依賴於以下幾點:
- SMPC 參與者可以包括「誠實但好奇」的參與者,他們可以通過與其他節點通訊來嘗試訪問任何底層資訊。
- SMPC 網路的安全性依賴於參與者正確執行協議並不故意引入錯誤或惡意行為的假設。
- 某些 SMPC 協議可能需要一個可信的設定階段來生成加密引數或初始值。這裡的信任假設是可信設定被誠實執行。
- 與 SMPC 網路相同,安全假設保持不變,但由於 OTM(Off-The-Grid Multi-party Computation)的存在,不存在「誠實但好奇」的參與者。
OTM 是一種多方計算協議,旨在保護參與者的隱私。它通過使參與者在計算中不公開其輸入資料來實現隱私保護。因此,「誠實但好奇」的參與者不會存在,因為他們無法通過與其他節點通訊來試圖訪問底層資訊。
有明確的贏家嗎?我們不知道。但每種方法都有自己的優點。雖然 NMC 看起來像是 SMPC 的明顯升級,但該網路還沒有上線,也沒有經過實戰測試。
使用 ZK 可驗證計算的好處是它是安全和隱私保護的,但它沒有內建的祕密共享功能。證明生成和驗證之間的不對稱使它成為可驗證外包計算的理想模型。如果系統使用純粹的 zk 驗證計算,則電腦 (或單個節點) 必須非常強大才能執行大量計算。為了在保護隱私的同時啟用負載共享和平衡,必須有祕密共享。
在這種情況下,像 SMPC 或 NMC 這樣的系統可以與像 Lurk 或 RiscZero 這樣的 zk 生成器相結合,以建立強大的分散式可驗證外包計算基礎設施。
當今的 MPC/SMPC 網路是中心化的,這一點變得尤為重要。目前最大的 MPC 提供商是 Sharemind,它上面的 ZK 驗證層可以證明是有用的。去中心化 MPC 網路的經濟模型尚未跑通。理論上,NMC 模式是 MPC 系統的升級,但我們還沒有看到其成功。
在 ZK 證明方案的競賽中,可能不會出現贏家通吃的情況。每種證明方法都針對特定型別的計算進行了優化,並且沒有一個適合所有型別的模型。計算任務的型別有很多種,也取決於開發人員在每個證明系統上做出的權衡。筆者認為基於 STARK 的系統和基於 SNARK 的系統以及它們未來的優化在 ZK 的未來都有一席之地。
(原文作者:Siddharth Rao,IOSG Ventures;特此感謝 Lurk Labs 的 John Burnham 對本文提出的寶貴意見與建議。)
📍相關報導📍
V神發表「zk-EVM多客戶端」:可保護以太坊L1,透過AI加速證明、容錯
Taiko項目詳解:被紅杉中國看重的Type-1 zkEVM







